研究成果
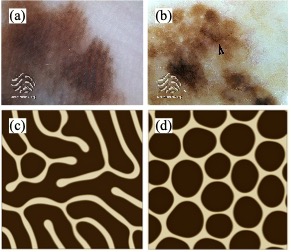
皮膚がんのパターン形成
皮膚に形成されるメラノーマは病理学的な観察が比較的容易であり、「縞状パターン」や「斑点パターン」などが知られている。本研究では、皮膚がんの形態形成を新しいタイプの「相分離現象」と捉えて、その形態形成を計算機シミュレーションによって調べた。その結果、細胞の増殖率と流体効果の強さの組み合わせによって異なるパターンが得られることがわかり、特徴的な長さをもつ縞状パターンや斑点パターンなどを再現することに成功した。
- T. Hoshino, M.-W. Liu, K.-A. Wu, H.-Y. Chen, T. Tsuruyama, and S. Komura, "Pattern formation of skin cancers: Effects of cancer proliferation and hydrodynamic interactions", Phys. Rev. E 99, 032416 (13pp) (2019). [PDF]
- 皮膚がんの形態形成の数理モデルを開発: 細胞の増殖効果と流体効果 (2019.3.25)
スイマー・マイクロレオロジー
ソフトマターのような粘弾性体中を遊泳するマイクロマシン(スイマー)の動作機構について調べ、スイマーの遊泳速度とソフトマターの粘性率や弾性率を結びつける関係式を理論的に導出した。この関係式に基づくと、ソフトマター中のスイマーの運動では「ホタテ貝の定理」が破れることや、スイマー自身の構造非対称性が重要であることが明らかになった。スイマーを用いて粘性や弾性を調べる新しい測定概念は「スイマー・マイクロレオロジー」と命名され、本研究によりその基本原理が与えられた。
- K. Yasuda, R. Okamoto, and S. Komura, "Swimmer-microrheology", J. Phys. Soc. Jpn. 86, 043801 (4PP) (2017). [PDF]
- K. Yasuda, R. Okamoto, and S. Komura, "A three-sphere microswimmers in a structured fluid", EPL 123, 34002 (6pp) (2018). [PDF]
- 構造流体中のマイクロスイマーの遊泳原理を解明:ゼリーの中で泳ぐには (2018.8.29)
- ソフトマター中のマイクロマシンの新しい遊泳機構を発見:「およげ!ホタテくん」 (2017.3.19)
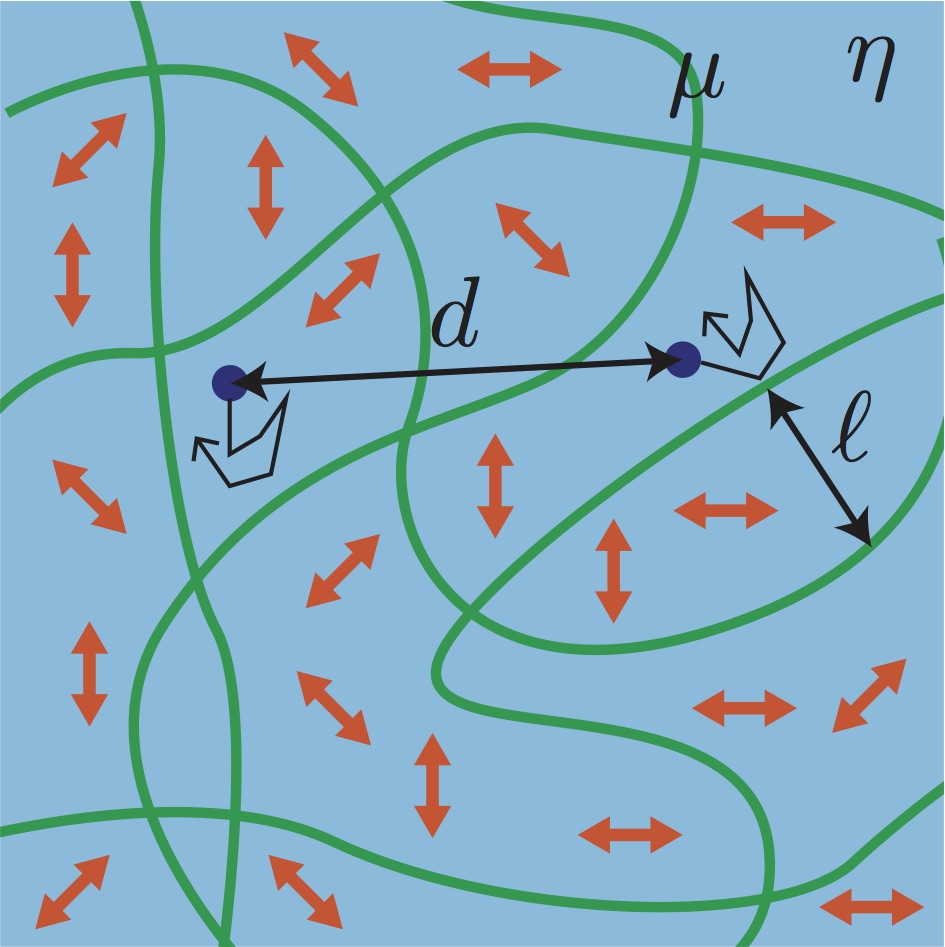
細胞中の異常拡散とマイクロレオロジー
アクティブな力双極子を有する粘弾性体中のブラウン運動について検討した。粘弾性体は二流体モデルで記述し、タンパク質を模倣したアクティブな力双極子の相関は特徴的な緩和時間をもつとした。プローブ粒子の平均二乗変位を計算した結果、熱ゆらぎのみ存在する場合、平均二乗変位は時間の0乗から1乗の間で変化することを求めた。一方、アクティブな力双極子によって、平均二乗変位は時間の0乗から2乗の間の全ての異常拡散が起こることを導いた。我々の結果は、近年の細胞中の異常拡散の振る舞いを適切に説明しており、生きている細胞と死んだ細胞では異常拡散のメカニズムが異なることが明らかになった。
- K. Yasuda, R. Okamoto, S. Komura, and A. S. Mikhailov, "Localization and diffusion of tracer particles in viscoelastic media with active force dipoles", EPL 117, 38001 (7pp) (2017). [PDF]
- K. Yasuda, R. Okamoto, and S. Komura, "Anomalous diffusion in viscoelastic media with active force dipoles", Phys. Rev. E 95, 032417 (14pp) (2017). [PDF]
脂質二重膜の緩和ダイナミクス
二種類の脂質からなる二重膜を「曲げ弾性をもった二成分流体」としてモデル化し、その動的挙動を調べた。膜外部の流体力学方程式と膜自身の流体力学方程式を連立させて解くことにより、膜の運動の緩和率を導出した。膜は曲げ弾性を持つとし、膜間では摩擦が生じると考える。また、膜の曲げによって脂質密度が平均の値からずれること(脂質密度と膜の曲げのカップリング)も考慮した。加えて我々は、二成分系に拡張するにあたり、膜内や膜間での脂質の相互作用の効果を導入した。計算の結果、五つの緩和モードを得た。そのうちの三つは、膜の曲げと結合した緩和モードであり、残りの二つは曲げとは結合しない。二成分に拡張したことによって、以前に得られていた緩和モードに加えて、新たに相互拡散に起因する二つの新たな緩和モードが現れる。特に、相分離臨界点近くにおいてはこれらのモードが他のモードに比べてはるかに遅い緩和モードとなることがわかった。
また、圧縮性のある脂質二重膜の緩和ダイナミクスの詳細な解析を行い、特にベシクル内外の粘性率の非対称性の効果を調べた。自由エネルギーの解析の結果、脂質密度と膜曲率の幾何学的な結合により、長波長と中間的波長で起こる二種類の不安定性が存在することがわかった。二重膜ベシクルのダイナミクスについては、オンサーガーの変分原理に基づいた厳密な定式化を行った。我々は球面調和関数表示を用いて、三つの連動する緩和率を解析的に求め、複数のモード交差現象が生じることを確認した。特にベシクルの内側の粘性率が外側と比べて大きくなると、曲げモードとスリップモードのクロスオーバーが短波長側に大きくシフトすることがわかった。我々は得られた結果を用いて、脂質二重膜ベシクルのゆらぎのパワースペクトルを計算し、さらに非熱的なゆらぎが働く場合のスペクトルの変化を検討した。
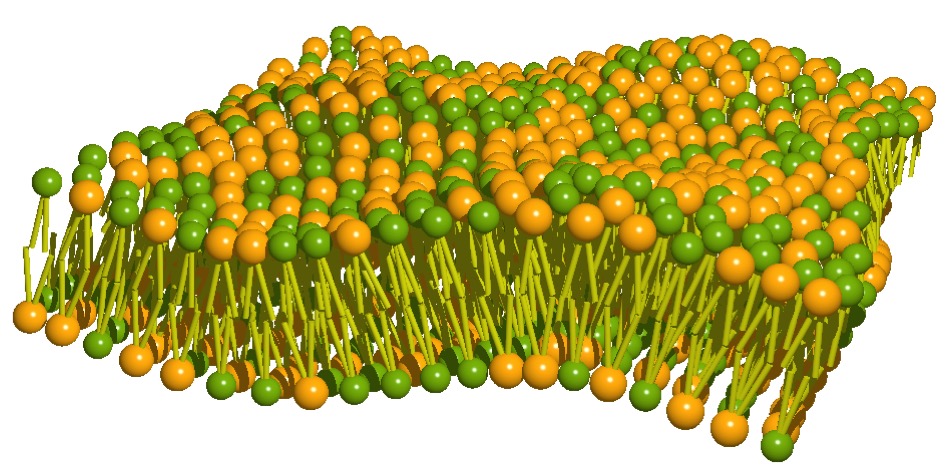
- R. Okamoto, Y. Kanemori, S. Komura, and J.-B. Fournier, "Relaxation dynamics of two-component fluid bilayer membranes", Eur. Phys. J. E 39, 52 (21pp) (2016). [PDF]
- T. V. Sachin Krishnan, R. Okamoto, and S. Komura, "Relaxation dynamics of a compressible bilayer vesicle containing highly viscous fluid", Phys. Rev. E 94, 062414 (14pp) (2016). [PDF]
生体膜の構造と相挙動
生体膜は脂質、ステロール、タンパク質などの様々な成分で構成されており、細胞の機能にとって不可欠な役割を果たしている。我々は生体膜の構造と相挙動に関して、多くの問題を扱ってきた。具体的には、フラストレーションによって誘起されるリップル相、脂質とコレステロールを含む生体膜における相転移と相分離、多成分脂質膜における張力誘起の形態転移、荷電脂質膜における電解質の添加効果、多成分脂質膜における粘着誘起の相分離、荷電脂質膜における相分離、カイラルな脂質分子が形成するヘリカル構造などがある。また、ダイナミクスに関しては、球状ベシクルの動的な形状ゆらぎ、ベシクル分散溶液の粘弾性などの研究を行なってきた。ここでは、変調された二重膜の結合効果について簡単に説明する。
最近、ワシントン大学の研究グループが、二枚の独立な多成分の脂質単層膜を貼り合わせて二重膜を構築することに成功した。その結果、二枚の単層膜間の結合効果が二重膜の相挙動に重要な影響を与えていることがわかった。我々はこの実験に触発されて、組成が周期的に変動する二枚の脂質単層膜の結合を記述するモデルを提案し、詳細な解析を行った。我々は平均場理論を用いて、変調された二重膜の相図を決定し、一方の膜の変調が他方の膜の変調を誘起することを確認した。また、二枚の膜で変調の周期が異なる場合には数値シミュレーションを実行し、周期の不整合性に起因するフラストレーションによって、複雑なモルフォロジーが出現することがわかった。このような現象は実験的にも観察されている。

- Y. Hirose, S. Komura, and D. Andelman, "Coupled modulated bilayers: A phenomenological model", ChemPhysChem 10, 2839-2846 (2009). [PDF]
- S. Komura, H. Shirotori, P. D. Olmsted, and D. Andelman, "Lateral phase separation in mixtures of lipids and cholesterol systems", Europhys. Lett. 67, 321-327 (2004). [PDF]
生体膜における流体力学的効果
生体膜を構成する脂質分子は液晶状態にあるため、一般に生体膜は流動性をもつ。生体膜に埋め込まれたタンパク質などは側方拡散で運動することが知られている。ただし、脂質二重膜は孤立した二次元系ではなく、周囲の溶媒(典型的には水)と結合している。このような生体膜において、構成成分は生体膜中で一様に分布しているのではなく、膜内の相分離によって特定の脂質やコレステロールを多く含むドメインを形成していることが明らかになりつつある。このドメインはタンパク質を選択的に取り込む機能を持つため、生物学において「ラフト」と呼ばれ、大きな関心を集めている。私は多成分の生体膜のダイナミクスにおける流体力学的効果に着目し、以下の研究成果を得た。
我々は運動量の緩和を含む二次元の流体力学的方程式を用いて、液体ドメインとマトリックスの粘性率が異なる場合に、液体ドメインの拡散係数のドメインサイズ依存性を解析的に求めた。その結果、ドメインサイズが小さい極限では対数的に依存するが、サイズが大きい場合には冪的(二乗)に減少することがわかった。また、ドメインの粘性率が小さいほど内部の流動が誘起され、ドメインの抵抗係数が小さくなることを示した。次に散逸粒子動力学シミュレーションの手法を用いて、二次元膜の相分離に対する三次元的な溶媒の効果を調べた。相分離は二次元面内で進行するにもかかわらず、溶媒の存在によってドメインの成長則が二次元的な指数から三次元的な指数に変化することを見出した。さらに三次元的な溶媒の存在下では、膜を構成する粒子の相関拡散の距離依存性が、対数的な依存性から冪的な依存性に変化することがわかった。これらの結果から、膜内の相分離が拡散と融合のメカニズムによって進行していることが明らかになった。一方、二成分流体膜の転移点直上における濃度ゆらぎのダイナミクスを考察し、濃度ゆらぎの減衰率の波数依存性を計算した。特に壁に挟まれた膜の場合、減衰率を解析的に計算することに成功した。その結果、実効的な拡散係数は高波数の極限で対数的にしか依存しないことが示された。
関連する研究として、二枚の流体膜が平行に配置されると、間に存在する三次元流体を通して膜間に流体力学的な結合が生じることを示した。すなわち、一方の膜内での運動が他方の膜内での運動を引き起こす。我々は相関拡散係数の解析的な表式を得た上で、膜間距離依存性を数値的に検討した。一方、二次元流体膜中に閉じ込められた高分子鎖のダイナミクスを解析し、特に周囲の溶媒による流体力学的効果を議論した。具体的には高分子鎖の緩和時間、拡散係数、動的構造因子などを計算した。ここでは、自由な膜と壁に挟まれた膜の両極限を考察した。高分子のサイズが流体力学的遮蔽長よりも大きくなると、自由な膜ではジムモデル、壁に挟まれた膜ではラウスモデルの結果と一致することを示した。さらに最近では、粘弾性体に挟まれた生体膜中のブラウン運動ついて考察して、新しいマイクロレオロジーの手法を理論的に提案した。
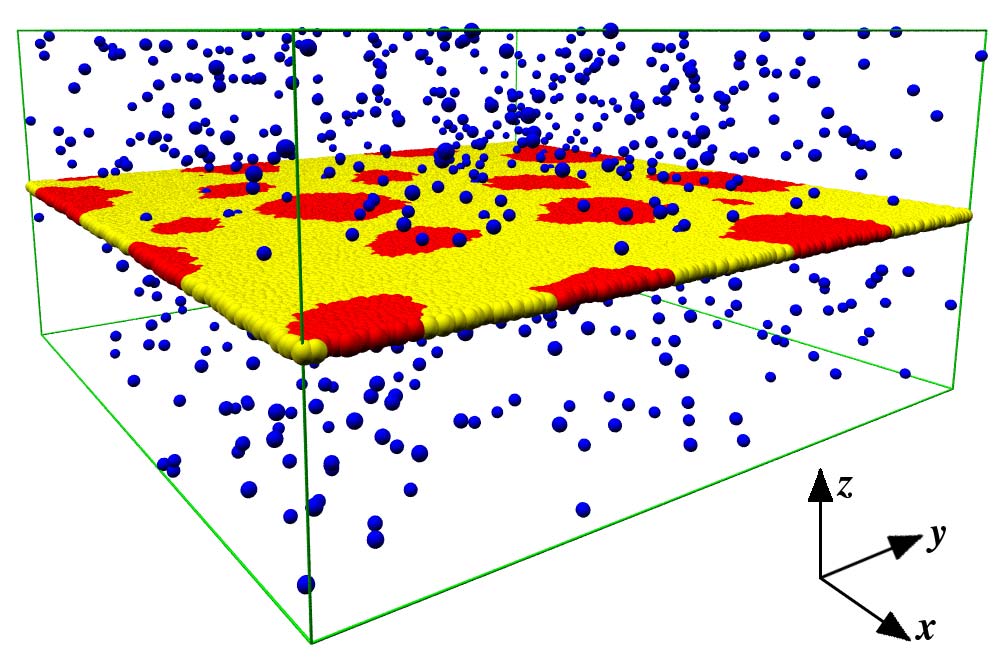
- S. Komura, S. Ramachandran, and K. Seki, "Anomalous lateral diffusion in a viscous membrane surrounded by viscoelastic media", EPL 97, 68007 (6pp) (2012). [PDF]
- S. Ramachandran, S. Komura, and G. Gompper, "Effects of an embedding bulk fluid on phase separation dynamics in a thin liquid film", EPL 89, 56001 (6pp) (2010). [PDF]
マイクロエマルションのメソスケール構造とダイナミクス
水、油、界面活性剤から成るマイクロエマルションでは、温度や組成を変化させることによって、様々なメソスケール構造を形成されることが知られている。界面活性剤の濃度が比較的高いと、ラメラ相、ヘキサゴナル相、キュービック相などの液晶相が出現する。界面活性剤の濃度を下げると、マイクロエマルションはランダムな双連結構造をとることが知られている。我々はマイクロエマルションの構造とダイナミクスに関して、複数の研究を行なってきた。具体的には、マイクロエマルションにおける超音波吸収、マイクロエマルションにおける形態転移とエマルション化失敗、マイクロエマルションの二秩序変数モデル、マイクロエマルションにおける添加高分子誘起のネマチック転移などがある。
近年では、高分子のホモポリマーとブロックコポリマーの混合系も、低分子系のマイクロエマルションと類似した構造形成を示すことが報告されている。実験的にも、高分子三元系において長距離秩序を持たない双連結構造が見つかっており、「高分子マイクロエマルション」と呼ばれている。このような興味深い構造形成のメカニズムを解明するために、我々は実空間における平均場理論を用いて、二種類のホモポリマーと対称なジブロックコポリマーの混合系の相分離構造について詳細に調べた。我々は、平均場理論が与える方程式を計算機上で直接的に解くことにより、双連結構造が出現する物理的要因を調べ、熱ゆらぎによらないランダム構造の存在を提唱した。
また、低分子マイクロエマルションに両親媒性のブロックコポリマーを添加すると、可溶化度が飛躍的に向上するという実験結果に触発され、二種類の両親媒性分子から成る混合ブラシのスケーリング理論を構築した。具体的には混合単層膜の曲げ弾性率や自発曲率などを計算し、二種類の純成分の物理量を内挿する非線型なスケーリング関数を求めた。さらにその結果を用いて、球状エマルションの平衡状態における界面量、界面曲率、混合自由エネルギーなど解析した。これにより、可溶化度上昇の物理的機構が明らかになった。

- S. Komura, "Mesoscale structures in microemulsions", J. Phys.: Condens. Matter 19, 463101 (30pp) (2007). [PDF]
- H. Kodama, S. Komura, and K. Tamura, "Mean-field approach to polymeric microemulsions", Europhys. Lett. 53, 46-52 (2001). [PDF]
ピッカリング・エマルションの安定性とダイナミクス
近年、界面活性剤の代わりに、コロイドなどの微粒子を用いてエマルションを安定化させる方法が注目されており、このようなエマルションのことを「ピッカリング・エマルション」という。このエマルションの興味深い点は、コロイド粒子の表面は化学的にほぼ均一であるにもかかわらず、適当な条件のもとで水と油の界面に吸着して、界面を安定化させることである。ピッカリング・エマルションの生成で最も重要な要素は粒子の濡れ性であり、二つの液体に対する濡れ性がバランスすると、粒子は界面に吸着して界面を安定化させる。最近はナノ技術の飛躍的な進歩により、粒子表面の化学的性質を部分的に変化させることも可能であり、親水部と疎水部をもつ粒子は「ヤヌス粒子」と呼ばれて、様々な応用も期待されている。
ピッカリング・エマルションの簡単なモデルとして、我々は球面状の液液界面に吸着する球状固体粒子の振る舞いを考察した。界面エネルギーと体積エネルギーの両方を考えることによって、平衡状態における粒子の接触角は古典的なヤングの式で与えられることを確認した。しかしながら、吸着エネルギー自体は界面の曲率に依存することがわかった。この結果を用いて、我々は球状粒子が二つの液体と界面の間でどのように分配されるかを計算した。粒子の分配は、粒子の濡れ性パラメータと界面曲率の関数として表される。我々は同様の計算をヤヌス粒子に対しても行い、ヤヌス粒子の場合には粒子の吸着によって界面の自発曲率が生じることがわかった。
また、平坦な液液界面への球状粒子の吸着ダイナミクスについてもモデル化と解析を行った。このような研究はピッカリング・エマルションの生成過程を知る上で重要である。自由エネルギーを用いた定式化により、我々は界面被覆率の時間発展と動的界面張力を計算した。吸着に要する特徴的時間を評価することにより、拡散律速型の吸着が起こることを明らかにした。また、平衡状態への漸近の仕方は、時間の逆数の平方根に比例することも示した。さらに、界面被覆率と界面張力を結びつける平衡状態における状態方程式は、一般に非平衡状態でも成り立つことを明らかにした。
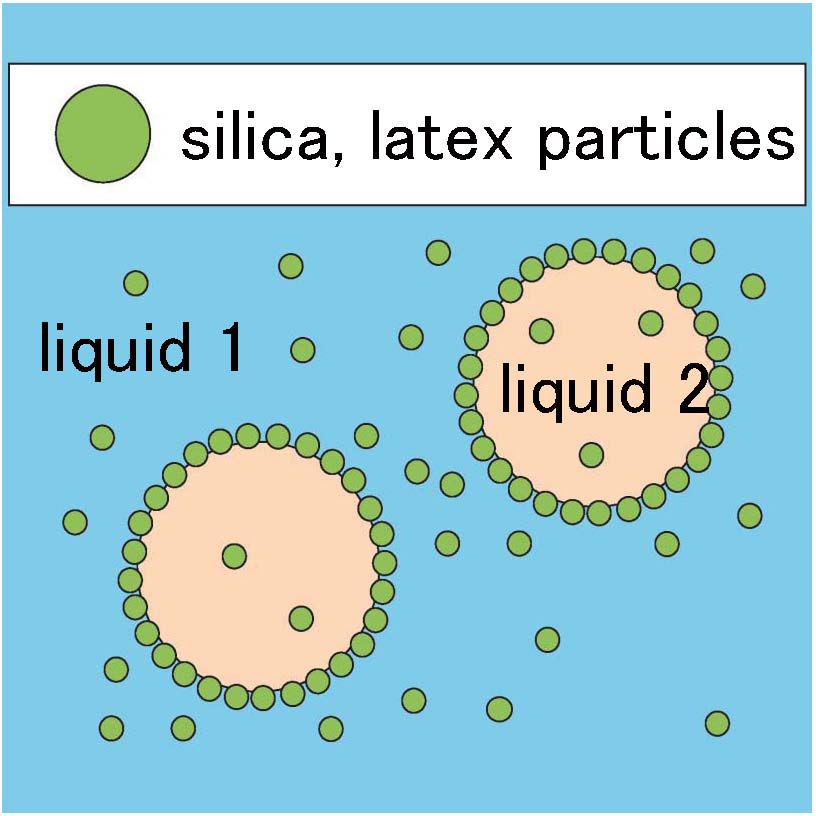
- Y. Hirose, S. Komura, and T. Kato, "Adsorption dynamics in Pickering emulsions", Prog. Theor. Phys. 175, 81-92 (2008). [PDF]
- S. Komura, Y. Hirose, and Y. Nonomura, "Adsorption of colloidal particles to curved interfaces", J. Chem. Phys. 124, 241104 (2006). [PDF]
構造レオロジー
ソフトマターの重要な特徴の一つは、物質内部にメソスケールの構造が自発的に形成されることである。その結果として、ソフトマターは非常に脆く、小さな外力でも大きな変形が誘起される。また、外力によってメソ構造が破壊されると、そのレオロジー的性質も著しく変化する。ところが、ソフトマターのメソ構造が関与するレオロジーの統一的な理論は、ごく一部の研究例を除いて物性物理学としていまだに存在しない。我々はこのような研究を「構造レオロジー」と呼んで、実験と理論の両面からのアプローチを行なっている。
我々は、最も単純なメソ構造として、一次元的なラメラ構造(リオトロピック系)またはスメクチック構造(サーモトロピック系)に着目し、そこに生じる転位などの欠陥構造の生成、消滅、運動に着目した理論を構築し、さらに理論的予測を実験的に検証してきた。特に最近では、実験的に得られた動的貯蔵弾性率の値を、ずり速度と換算温度の組み合わせによって整理して、スケーリングの関係が成り立つことを確かめた。一方、独立の顕微鏡観察によりフォーカルコニックドメインの大きさを測定して、貯蔵弾性率と同様に、ずり速度と換算温度を組み合わせた独立のスケーリング関係を見出した。これらの二つのスケーリング関係が両立するためには、貯蔵弾性率とフォーカルコニックドメインの大きさが反比例する必要があることがわかった。また次元解析から、その比例係数はスメクチック相の曲げ弾性率と層圧縮弾性率で与えられる表面張力に対応していることもわかった。以上のことから、フォーカルコニックドメインを含むスメクチック相の弾性は本質的に表面張力で支配されていることを示した。同様な現象はリオトロピック液晶相のオニオン相でも見られ、欠陥構造を媒介とするレオロジーにおける普遍的な描像を得ることに成功した。

- S. Fujii, S. Komura, Y. Ishii, and C.-Y. D. Lu, "Elasticity of smectic liquid crystals with focal conic domains", J. Phys.: Condens. Matter 23, 235105 (7pp) (2011). [PDF]
- S. Fujii, Y. Ishii, S. Komura, and C.-Y. D. Lu, "Smectic rheology close to the smectic-nematic transition", EPL 90, 64001 (6pp) (2010). [PDF]
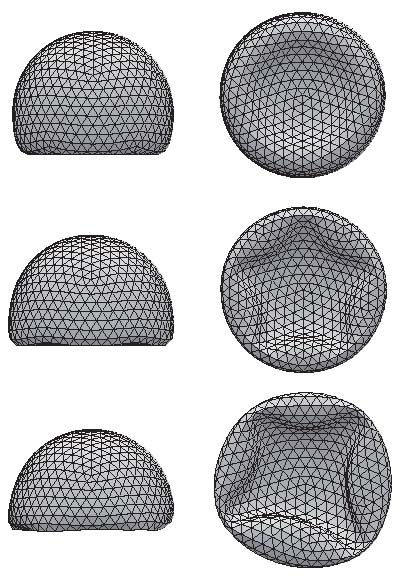
弾性的な薄膜の大変形理論とシミュレーション
弾性的な薄膜の変形や構造の研究は、フラーレン、ウィルス、ラングミュア単分子膜、細胞骨格などの形態とも密接に関係しており、また実用や応用の観点からも重要である。弾性的な薄膜に大きな外力を加えると座屈現象が起こり、構造が劇的に変化する。弾性的な薄膜の重要な性質の一つは、伸長に要するエネルギーが曲げに要するエネルギーよりもはるかに大きいということである。そのため、伸長を伴わない曲げ変形が容易に起こる。この問題に対して、我々は弾性ベシクルのモンテカルロ・シミュレーション、円筒状の弾性ベシクルのゆらぎと形状安定性の解析などを行なった。特に球状弾性殻の吸着変形については詳細に検討したので、それについて以下で述べる。
我々はファン・デル・ワールス力によって固体基盤に吸着する弾性殻の変形を数値計算によって調べた。弾性殻の形態は、伸長弾性率と曲げ弾性率の二つのパラメータによって特徴付けられる。吸着エネルギーと弾性エネルギーの競合により、複数の変形のパターンがあることがわかった。また、伸長弾性率の大小に応じて、不連続的または連続的な座屈転移が起こることを示した。我々は、スケーリング解析を行うことにより、球殻のへこみ長が殻の実効的な厚さを超えるときに座屈転移が起こることを明らかにした。さらに転移点においては、へこみ長と殻の厚さの比が2〜3の普遍的な値になる。このような普遍的な値は、ナノスケールの球殻(フラーレン)から巨視的スケールの球殻(ピンポン球)において実験的にも観察されている。関連する研究として、弾性チューブの基盤吸着の問題も検討し、球殻とは異なる振る舞いを示すことがわかった。